The XY-Chain strategy allows you to eliminate candidates in a manner similar to Y-Wing.
How to Use XY-Chain
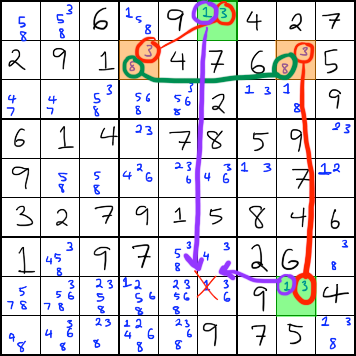
To use XY-Chain, look for two bi-value cells (we'll call them "pincers") that can't see each other but that have at least one number in common (we'll call it the "shared number.") In the example below, our pincers are light green, and both of them have the same candidates.
If the pincers can both see cells that contain the shared number, you might be able to eliminate the shared number from those cells that the pincers can see.
However, in order to do this, you have to form a chain between the two pincers.
In the above example, the light green squares are the pincers. They can't see each other. They both contain the number 1, and they can both see the number 1 in another cell (the purple arrows are pointing to it.) They can also see cells that contain 3, but we will try to form a chain that eliminates 1.
To form a chain, you start with one of the pincers and use the candidate that you aren't trying to eliminate elsewhere. In this case, we are trying to eliminate a 1, so we will start the chain with the number 3.
The links in an XY-chain have to all be bi-value cells. Our starting pincer can see a bi-value cell that contains a 3, so we can connect the pincer to that cell.
Then we use the other number in that cell (in this case 8) to connect to another bi-value cell that it can see. In this case, we can connect to another cell in the row that contains 3 and 8.
Finally, we can connect to the other pincer near the bottom-right of the grid. Since we formed a connection, we can eliminate the 1 from the cell that the pincers can see.
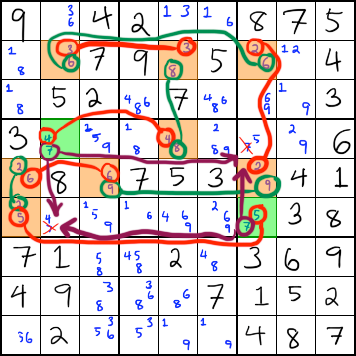
In the example below, you can see that XY-chains can be pretty long and complicated, and they can remove more than one candidate if the pincers can see more than one of them.