X-Wing is a strategy in which you find a candidate that appears twice in two different rows, and those appearances are both in the same column, OR, the candidate appears twice in two different columns, and those appearances are both in the same row.
X-Wing Example
When a candidate appears twice in the same row, you know that that candidate must be in one of those two squares. If there is a second row where that candidate appears exactly twice, then you know that the candidate must be in one of those two squares in that row.
If those candidates are also on the same column, as is the case with the 2 in the picture below, then the solved 2s will be diagonally across from each other, as shown in the picture below. This crossing diagonal pattern is where the name "x-wing" comes from.
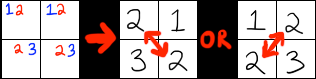
See the X-Wing example below:
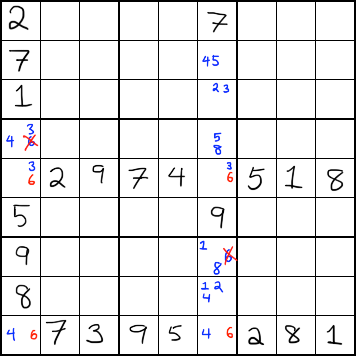
As with the above illustration, the candidate 6 (shown in red) appears twice in two different rows, and only twice. In addition, those 6s are also aligned on the same column. However, there are other 6s in those columns.
Since the 6s in the marked rows are the only two in their respective rows, you know that the 6s must occur in one of those two squares in those rows. As illustrated above, you know that once you figure out where to place one of the 6s, the other 6 will be diagonally across from it.
Whichever way you place the 6s, though, you know that they can't appear in any other cell in their columns, because they have to be in those two rows. If a 6 were placed anywhere else in those columns, it would prevent 6 from appearing in one of those rows. For that reason, you can eliminate any 6s in those columns that aren't in those two rows. Those 6s are shown crossed out in red.
X-Wing also works the other way, with candidates that appear only twice in two columns, with both aligned on the same rows.
Example Puzzle
There are two X-Wings in the following puzzle.