3D Medusa is a coloring strategy similar to simple coloring. It allows you to eliminate candidates.
How to Use 3D Medusa
3D Medusa starts like Simple Coloring. You choose a candidate, assign it a color, then assign the opposite color to other candidates, alternating colors until you have discovered eliminations.
However, 3D Medusa is more complicated. It makes use of bi-value cells to expand the coloring to a bigger network of candidates. The bi-value coloring used in the 3D Medusa strategy is similar to that in XY-Chains.
You can start 3D Medusa by giving alternate colors to candidates that share a strong link (see the page on X-Cycles for an explanation of strong links). Keep following strong links and assigning colors until you color a candidate in a bi-value cell. Now that you have colored it, you can give the opposite color to the other candidate in the bi-value cell.
Note that a sudoku grid can have multiple 3D medusas in it. If you color a 3D medusa and don't find any eliminations, you can start a new medusa with a candidate that wasn't colored in any previous 3D medusas.
After you have colored all the cells that are connected in the network of strong links and bi-value cells, you can look for candidates that can be eliminated, based on the following rules.
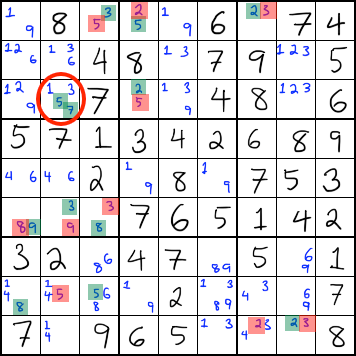
Same color twice in a cell
If the same color occurs twice in a cell in a 3D Medusa, then it's a contradiction, and you can remove all candidates with that color.
As you can see in the above example, the circled cell contains two green candidates. Since the colors represent two possible ways to solve the grid, it means that either all of the green candidates are correct or all of the red candidates are correct. However, for the green candidates to be correct, there would have to be two numbers in the circled cell, which is impossible. Therefore, none of the green candidates can be correct, so you can eliminate all of them.
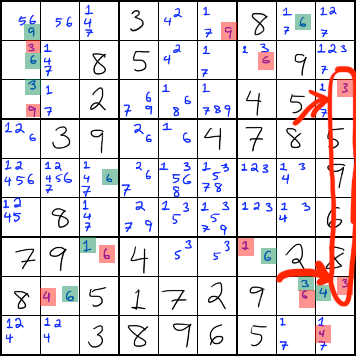
Same color twice in a unit
If the same color occurs twice in a row, column, or box, it is a contradiction (both numbers would have to be correct at the same time), so you can eliminate all candidates of that color.
In the example above, the circled 3s are both red. If red were the correct color, then both of those 3s would have to be correct, but that is a contradiction. Therefore, all red candidates can be eliminated.
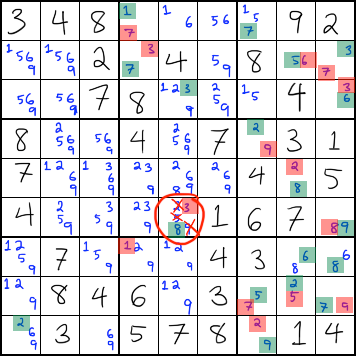
Two colors in a cell that contains uncolored candidates
If both colors of your 3D medusa occur in a cell that contains uncolored candidates, you can remove the uncolored candidates from that cell. This is because you know that one or the other color MUST be correct, so all uncolored possibilities in that cell must be invalid.
In the example below, the circled cell contains two oppositely-colored candidates. All the other candidates in that cell can be removed.
Two colors in a unit
If a candidate appears twice in a unit and if they are oppositely-colored, you can remove any uncolored versions of that candidate that the colored ones can see.
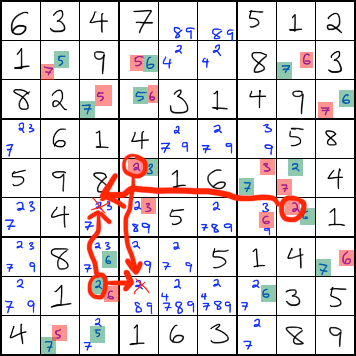
Uncolored candidate can see two oppositely-colored candidates
If an uncolored candidate can see two of the same candidate, and if those candidates are oppositely-colored, you can remove that uncolored candidate. In the example below, you can eliminate two 2s because each one can see both a red and a green 2.
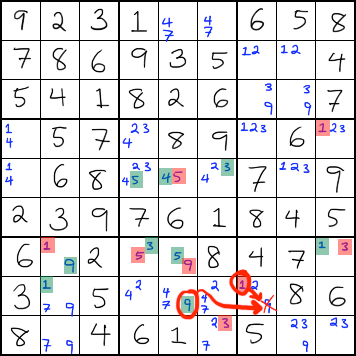
Uncolored candidate can see a colored one, and an oppositely colored candidate in the same cell
This one is a little confusing to explain. If an uncolored candidate can see a colored version of itself, and if the uncolored candidate shares a cell with a candidate (any number) that has the opposite color, then you can eliminate that candidate.
In the example below, there is a green 9 in the same row as an uncolored 9. The uncolored 9 is in a cell with a red number, which is the opposite color from the green 9. This combination allows you to remove the uncolored 9.