Intersection removal is a strategy where you can eliminiate one candidate from a cell or cells. There are two types of intersection removal: pointing pairs and box/line reduction. This page will deal with the second of those two.

Box/Line Reduction

You can use Box/Line reduction if a candidate only appears two or three times in a row or column, and those candidates are also all in the same box. When this happens, you know that the candidate MUST occur in that row or column because it can't appear anywhere else there, so it CAN'T occur elsewhere in that box.

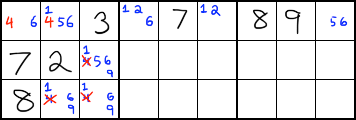
In the above example, the red 4s are the only 4s in their row. Those 4s also happen to occur together in the same box. The other 4s in the box cannot be valid because they would prevent a 4 from appearing in that row. When the puzzle is eventually solved, the 4 in that box and row MUST be one of the red 4s. Because of that, we can eliminate the other 4s that are in that box. They have been crossed out in red.

Example Puzzle

You can solve the following interactive puzzle using only the Box/Line Reduction strategy.

Example Puzzle 2

Here is another interactive puzzle that can be solved using only the Box/Line Reduction strategy.