Simple Coloring, also known as Singles Chains, is a strategy that allows you to eliminate candidates by looking for contradictions.
Conjugate Pairs
If a candidate appears EXACTLY twice in a unit, then those two candidates are called a conjugate pair.

In the above example, the 1s form a conjugate pair, and the 2s also form a conjugate pair.
With a conjugate pair, you know that the candidate MUST appear in one of those two squares. They have an either/or relationship.
When to use Simple Coloring
You can make use of Simple Coloring when a conjugate pair is "chained" with at least one other conjugate pair using the same candidate.
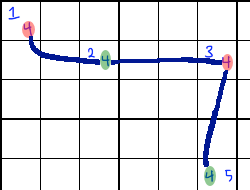
In the above example, 4 occurs exactly twice in the upper-left box, so it forms a conjugate pair in that box. Similarly, 4 occurs exactly twice in the second row, so it forms a conjugate pair in that row. The cell that has 2 and 4 in it is part of BOTH of those conjugate pairs, so these pairs form a chain. Similarly, 4 occurs exactly twice in the sixth column, so it forms a conjugate pair in that column. The cell with 3 and 4 in it is part of two conjugate pairs, continuing the chain. This chaining gives this strategy its alternate name of Singles Chains.
How to use Simple Coloring
When you find a chain of conjugate pairs, you might be able to use simple coloring to remove candidates. Start with one conjugate pair. Since the pair has an either/or relationship, you can give each candidate a different color.
Next, start from one of the colored numbers and look for a conjugate pair that it chains with. You can give the opposite color to the other number in the pair. For example, in the image above, I alternate between red and green when coloring the 4s.
Keep doing this until you have colored all of the numbers in the singles chain. Because of the either/or relationship of conjugate pairs, you know that if one color is correct, then the candidates of the other color can all be eliminated. So if the red 4 in the top-left corner turns out to be correct, we can erase not only the green 4 in its box, but also the green 4 at the bottom-right of the image. If this were a longer chain, we would remove all green 4s from the grid.
There are several ways to use simple coloring to eliminate candidates. They are described below.
Color Appears Twice in a Unit
If candidates of the same color appear together in the same unit, then you know that that color is incorrect, because if that color were correct, then that candidate would have to be in two places in one unit, which is not allowed. Therefore, all of the candidates of that color can be eliminated.
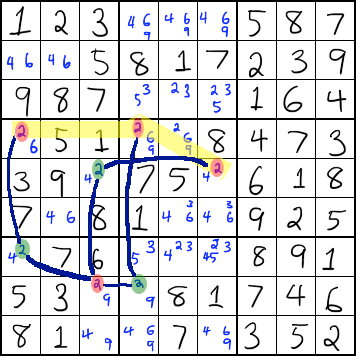
The above image shows an example of candidates of the same color appearing together in the same unit. The 2s that are highlighted in yellow are in the same units, but they are all the same color. Since we know that either ALL of the green or ALL of the red 2s will be "on," we know that the red 2s can't possibly be correct, because there would be more than one 2 in the same unit, as indicated by the yellow highlight. Therefore, all of the red 2s can be eliminated--even the one that is not highlighted in yellow.
In the following puzzle, some 1s can be removed because of a color appearing twice in a unit.
Opposite Colors in the Same Unit
The chain formed by the colored pairs might have several end points that don't connect with any other pairs. Sometimes, these chain ends appear together in the same unit, but they are of opposite colors, so they don't create a contradiction.
However, because of the either/or nature of conjugate pairs, you know that one of these end points must be the correct one. That means that, for example, if you colored a chain of 4s, and if two 4s of different colors appear together in the same unit, AND there are some uncolored 4s in that unit as well, then you can eliminate all of those uncolored 4s.
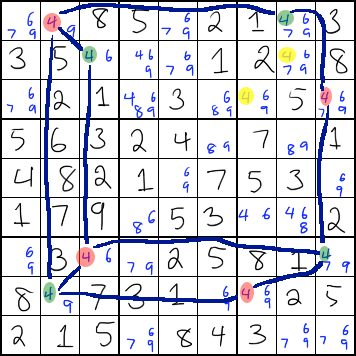
Above is an example where you can use simple coloring this way. The 4s in the top-right are opposite colors, and they are in the same box together. There are some uncolored 4s in that box (highlighted in yellow). However, you know that the only valid 4s in that box are the ones that you have colored in. Therefore, you can eliminate those yellow 4s.
An Uncolored Candidate can See Two Oppositely-Colored Candidates
If an uncolored candidate is in the same unit as a colored candidate, it can be described as "seeing" that colored candidate. In the picture below, there is an uncolored 2 (highlighted in yellow) that can see two colored ones (the purple arrows are pointing from them.) The colored candidates are opposite colors from each other. Because of this, you can eliminate the yellow 2. This is because you know that one of the colored 2s must be the correct one, and no matter which one it is, it will prevent that uncolored candidate from existing there.
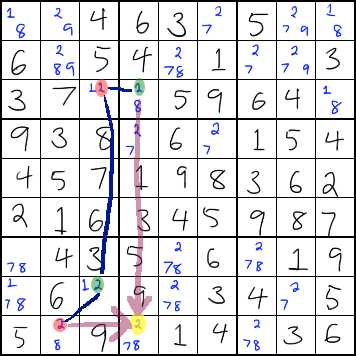
Here is a puzzle where two 6s can be removed because they can see two oppositely-colored 6s.