The final step to creating a QR Code is to create the format and version strings, then place them in the correct locations in the QR code. This page explains how to generate the format and version strings, and illustrates where they are placed in the QR code.
Format String
The format information string encodes which error correction level and which mask pattern is in use in the current QR code. Since there are four possible error correction levels (L, M, Q, and H) and eight possible mask patterns, there are 32 (4 times 8) possible format information strings. The next section explains how to generate these format strings. For a complete list of the 32 format strings, please refer to the format string table.
Generate the Format String
The format string is always 15 bits long. To create the string, you first create a five bit string that encodes the error correction level and the mask pattern in use in this QR code. Then you use those five bits to generate ten error correction bits. The resulting fifteen bits are XORed with the mask pattern 101010000010010. This process is explained in detail below.
The Error Correction Bits
The first step to creating the format string is to get the two bits that specify the error correction level in use in the QR code. The following table shows the bit sequences for each error correction level.
| Error Correction Level | Bits | Integer Equivalent |
|---|---|---|
| L | 01 | 1 |
| M | 00 | 0 |
| Q | 11 | 3 |
| H | 10 | 2 |
Notice that the numbers do not go in order of 0, 1, 2, 3 in the table.
The Mask Pattern Bits
For the mask patterns, refer to the QR code mask patterns page to find the mask number that goes with each pattern. Convert the number into a three-bit binary string.
Example Five Bit Format String
For example, if we have used error correction level L and mask pattern 4, the five-bit binary sequence is created like so:
01 (indicator for error correction level L)
100 (binary for 4, i.e. mask pattern 4)
Result: 01100
Generate Error Correction Bits for Format String
Now that we have five bits for the format string, we have to use it to generate ten error correction bits. This step uses Reed-Solomon Error Correction, but it is a little easier because in this case, the polynomials contain no more than fifteen terms, and their coefficients are all 1s or 0s.
Get the Generator Polynomial
When generating the format string's error correction codewords,
the QR code specification says to use the following generator polynomial:
x10 + x8 + x5 + x4 + x2 + x + 1
We can convert this to a binary string by taking only the coefficients of each term. The coefficient of x10 is 1, the coefficient of x9 is 0 because x9 isn't present in the polynomial, and so on.
In other words, the binary string that represents the generator polynomial
for this step is
10100110111
Calculate the Error Correction Bits
The next step is to divide the format string bits (01100 from the previous step) by the generator polynomial (10100110111 from the previous step).
To do this, first create a 15-bit string by putting ten 0s to the right of
the format string, like so:
01100 -> 011000000000000
Now remove any 0s from the left side:
011000000000000 -> 11000000000000
Now we perform the division.
The steps (described in more detail below) are:
1. Pad the generator polynomial string on the right with 0s to make it the
same length as the current format string.
2. XOR the padded generator polynomial string with the current format string.
3. Remove 0s from the left side of the result.
We must divide the polynomials until the resulting format string is 10 or fewer bits long. Therefore, before each division step, check to make sure that the current format string is 11 bits or longer (11 bits is the length of the generator polynomial). Our current string, 11000000000000, is 14 bits long.
First Division
First, pad the generator polynomial string
on the right with 0s to make it the same
length as the current format string:
10100110111 <-- generator polynomial with no padding
11000000000000 <-- current format string as shown in previous section
10100110111000 <-- padded generator polynomial
Now, XOR the format string with the padded generator polynomial:
11000000000000 ^ 10100110111000 = 01100110111000
And remove the 0s from the left side of the result:
01100110111000 -> 1100110111000
Second Division
The resulting string 1100110111000 is 13 bits long, so since that is 11 bits or longer, we can continue.
Pad the generator polynomial on the right to make the same length as the
current format string:
10100110111 <-- generator polynomial with no padding
1100110111000 <-- current format string
1010011011100 <-- padded generator polynomial
XOR the current format string with the padded generator polynomial: 1100110111000 ^ 1010011011100 = 110101100100
Third Division
The resulting string 110101100100 is 12 bits long, so since that is 11 bits or longer, we can continue.
Pad the generator polynomial on the right to make the same length as the
current format string:
10100110111 <-- generator polynomial with no padding
110101100100 <-- current format string
101001101110 <-- padded generator polynomial
XOR the current format string with the padded generator polynomial: 110101100100 ^ 101001101110 = 011100001010
And remove the 0s from the left side of the result:
011100001010 -> 11100001010
Fourth Division
The resulting string 11100001010 is 11 bits long, so since that is 11 bits or longer, we can continue.
There is no need to pad the generator polynomial, because the format string is now the same length.
XOR the current format string with the generator polynomial: 11100001010 ^ 10100110111 = 1000111101
The result is 10 bits long, so we are done with the division step. If the result were smaller than 10 bits, we would pad it on the LEFT with 0s to make it 10 bits long.
Put the Format and Error Correction Bits Together
Create a string using the original five bits of the format information (the error correction level indicator and the mask pattern indicator), followed by the error correction bits that we just generated.
The five-bit format string: 01100
The ten-bit error correction string from the division step: 1000111101
The combined string: 011001000111101
XOR with the Mask String
The QR code specification says to XOR the result with the following binary string: 101010000010010
011001000111101 ^ 101010000010010 = 110011000101111
The final format string for a code with error correction level L and mask pattern 4 is 110011000101111
For a list of all 32 format strings, refer to the format string table.
Put the Format String into the QR Code
The format information string is placed below the topmost finder patterns and to the right of the leftmost finder patterns, as shown in the image below. The number 0 in the image refers to the most significant bit of the format string, and the number 14 refers to the least significant bit. In other words, using the format string 110011000101111 from the example above, the numbers in the below image correspond to the format string bits as follows:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
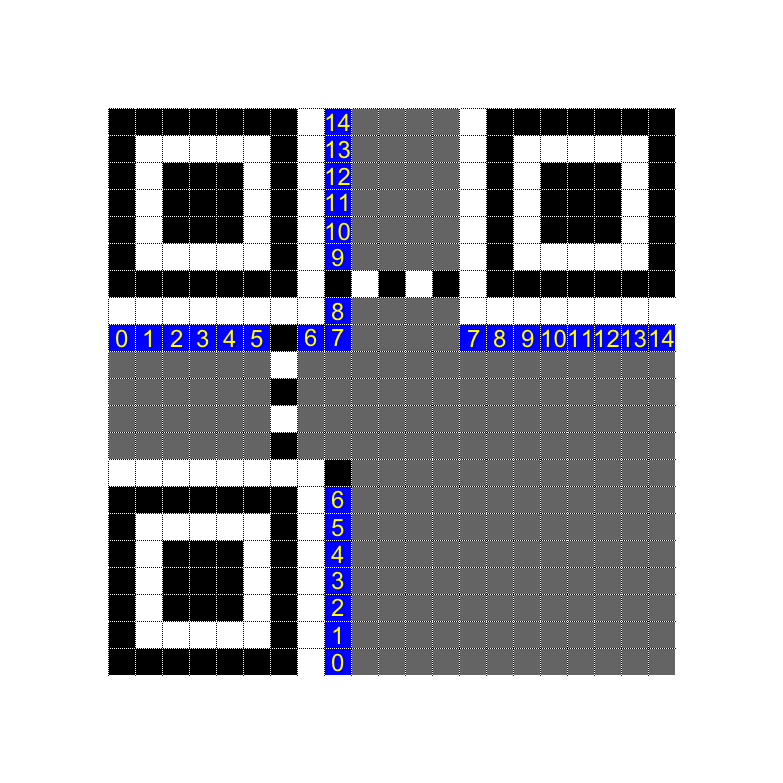
The image below shows the example format string, 110011000101111, in a version 1 QR code.

Dark Module
Every QR code must have a dark pixel, also known as a dark module,
at the coordinates (8, 4*version + 9).
That is, the y coordinate of the dark module is
version 1: 4*1 + 9 = 13
version 2: 4*2 + 9 = 17
version 3: 4*3 + 9 = 21
and so on.
This means that the dark module is always to the right of the top right corner of the bottom-left finder pattern. This is shown in the image below.
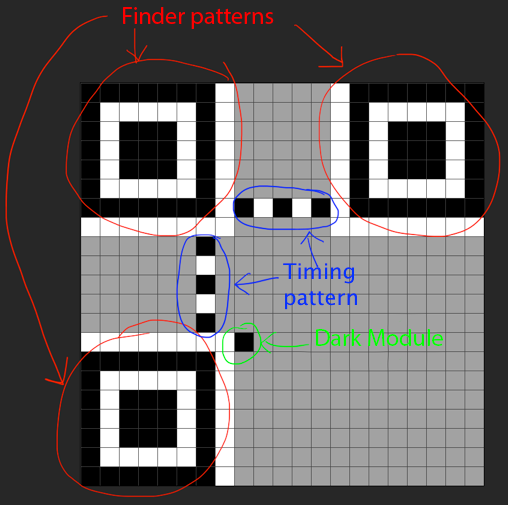
For Bigger Codes
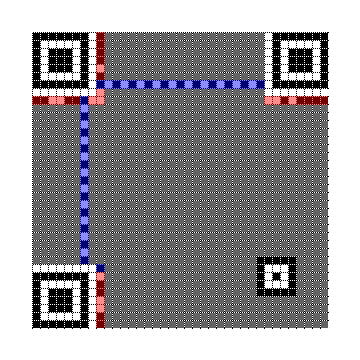
No matter what size the QR code is, the format string bits are placed below the topmost finder patterns and to the right of the leftmost finder patterns, as illustrated below. Note that both images have the same format string, 110011000101111, from the example earlier on this page. The format string is highlighted in red, and the timing pattern and dark module are highlighted in blue.

Version Information
If the QR Code is version 7 or larger, you must include an 18-bit version information string in the bottom left and top right corners of the QR code. (For a full list of all possible version information strings, refer to the format and version tables.) The version information areas are the 6x3 blue rectangles shown in the images below. The version information is placed beside the finder patterns no matter how large the QR code is. The image on the left is a version 7 code, and the image on the right is a version 22 QR code.


Generating the Version Information String
The QR Code specification says to use the (18, 6) Golay code for the version information string. As such, the version information string is an 18 bit string that consists of a six bit binary string that encodes the QR version, followed by a string of 12 error correction bits. The entire string is 18 bits long.
Get the Generator Polynomial
The QR code specification says to use the following generator polynomial
for this step:
x12 + x11 + x10 + x9 +
x8 + x5 + x2 + 1
As explained in the format string section earlier on this page,
we can represent this generator
polynomial with the following binary string:
1111100100101
Perform the Division
From here, we can follow the same division steps that we used to generate the format information string, except in this case we pad the initial strings to be 18 bits long rather than 15, and we stop when the current bit string is 12 or fewer bits long, rather than 10 or fewer.
Start by making a six bit binary string that represents the version number.
For example, for a version 7 code, the six bit binary equivalent of 7 is:
000111
Turn this into an 18 bit string by padding on the right with 0s:
000111000000000000
And remove the 0s from the left side:
111000000000000
Now pad the generator polynomial on the right with 0s to be the same length.
111000000000000 <-- version string
1111100100101 <-- generator polynomial with no padding
111110010010100 <-- padded generator polynomial
XOR the version string and padded generator polynomial:
1110000000000 ^ 111110010010100 = 110010010100
This string is already the required length of 12, so there is no further division required. As with the format information string, if the result is smaller than 12, it must be padded on the LEFT with 0s to make it 12 bits long.
Finally, put the original six bit version string to the left of the
result from the last step.
version string: 000111
error correction string from above: 110010010100
final version information string: 000111110010010100
For a full list of all possible version information strings, refer to the format and version tables.
Place the Version String in the QR Code
There are two rectangular areas where the version information string must be placed: one of the bottom left, and one on the top right.
Bottom Left Version Information Block
The bottom left version information block is 3 pixels tall and 6 pixels wide. The following table explains how to arrange the bits of the version information string in the bottom-left version information area. The 0 represents the RIGHTmost (least significant) bit of the version information string, and the 17 represents the LEFTmost (most significant) bit of the version information string.
| 00 | 03 | 06 | 09 | 12 | 15 |
| 01 | 04 | 07 | 10 | 13 | 16 |
| 02 | 05 | 08 | 11 | 14 | 17 |
Top Right Version Information Block
The top right version information block is 3 pixels wide and 6 pixels tall. The following table explains how to arrange the bits of the version information string in the top-right version information area. The 0 represents the RIGHTmost (least significant) bit of the version information string, and the 17 represents the LEFTmost (most significant) bit of the version information string.
| 00 | 01 | 02 |
| 03 | 04 | 05 |
| 06 | 07 | 08 |
| 09 | 10 | 11 |
| 12 | 13 | 14 |
| 15 | 16 | 17 |
Using the version 7 information string, 000111110010010100, as an example, the numbers in the above tables correspond to the bits as follows:
| 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
Example of Version 7 Information String
The following image is a version 7 QR code, which uses the version information string 000111110010010100. Notice that the version information areas are filled in according to the pattern described in the tables above.

Output the Final Matrix
The final step, after adding format and version information to the QR matrix, is to output the final matrix, using the mask pattern that was determined to have the lowest penalty score.
Add the Quiet Zone
Please note that the QR code specification requires that the QR matrix be surrounded by a quiet zone: a 4-module-wide area of light modules.
Final Output
The following image is a 1-Q code of HELLO WORLD, encoded in alphanumeric mode.

Conclusion
This concludes the QR code tutorial. In summary, QR codes are generated with the following steps:
- Determine which encoding mode to use
- Encode the data
- Generate error correction codewords
- Interleave blocks if necessary
- Place the data and error correction bits in the matrix
- Apply the mask patterns and determine which one results in the lowest penalty
- Add format and version information